Class 9th Science Chapter 8 गति

गति

प्रश्न श्रृंखला-1 # पृष्ठ संख्या 110
प्रश्न 1. एक वस्तु के द्वारा कुछ दूरी तय की गयी। क्या इसका विस्थापन शून्य हो सकता है? अगर हाँ, तो अपने उत्तर को उदाहरण के द्वारा समझाइए।
उत्तर: हाँ, विस्थापन शून्य हो सकता है।
उदाहरण: वृत्ताकार मार्ग पर गति करता हुआ कोई पिण्ड एक चक्कर लगाता है तो उसकी प्रारम्भिक एवं अन्तिम स्थिति एक ही है अतः विस्थापन शून्य है।
प्रश्न 2. एक किसान 10 m की भुजा वाले एक वर्गाकार खेत की सीमा पर 40 s में चक्कर लगाता है। 2 मिनट 20 सेकण्ड के बाद किसान के विस्थापन का परिमाण क्या होगा?
हल:
1 चक्कर में लगा समय = 40 s (दिया है)
कुल समय 2 मिनट 20 से. = 120 + 20 = 140 s

अर्थात् यदि किसान चित्रानुसार A से गति प्रारम्भ करता है, तो C पर यात्रा समाप्त करेगा अर्थात्
विस्थापन AC कर्ण होगा।
जिसका मान = वर्ग की भुजा x √2 = 10√2 मीटर = 14.14 मीटर
अतः अभीष्ट विस्थापन = 14.14 मीटर।
प्रश्न 3. विस्थापन के लिए निम्न में कौन सही है –
(a) यह शून्य नहीं हो सकता।
(b) इसका परिमाण वस्तु के द्वारा तय की गई दूरी से अधिक है।
उत्तर: उपर्युक्त कोई भी कथन सत्य नहीं है।
प्रश्न श्रृंखला-2 # पृष्ठ संख्या 112
प्रश्न 1. चाल एवं वेग में अन्तर बताइए।
उत्तर:  चाल और वेग में अन्तर:
चाल :-

1. एकांक समय में चली गई दूरी चाल कहलाती है।
2. चाल एक अदिश राशि है।
3. इसे व्यक्त करने के लिए केवल परिमाण की आवश्यकता होती है।
4. इसका औसत मान कभी भी ऋणात्मक या शून्य नहीं हो सकता।

वेग :-

1. एकांक समय में किसी निश्चित दिशा में विस्थापन वेग कहलाता है।
2. वेग एक सदिश राशि है।
3. इसे व्यक्त करने के लिए परिमाण एवं दिशा दोनों की आवश्यकता होती है।
4. इसका औसत मान शून्य, ऋणात्मक या धनात्मक हो सकता है।

प्रश्न 2. किस अवस्था में किसी वस्तु के औसत वेग का परिमाण उसकी औसत चाल के बराबर होगा?
उत्तर: जब वस्तु की गति एक निश्चित दिशा में सरल रेखीय होगी।
प्रश्न 3. एक गाड़ी का ओडोमीटर क्या मापता है?
उत्तर: गाड़ी द्वारा तय की गई दूरी।
प्रश्न 4. जब वस्तु एकसमान गति में होती है तब इसका मार्ग कैसा दिखाई देता है?
उत्तर: एक सरल रेखा।
प्रश्न 5. एक प्रयोग के दौरान अन्तरिक्ष यान से एक सिग्नल को पृथ्वी पर पहुँचने में 5 मिनट का समय लगता है। पृथ्वी पर स्थित स्टेशन से इस अन्तरिक्ष यान की दूरी क्या है? (जबकि सिग्नल की चाल = प्रकाश की चाल = 3 x 108 m s^-1)
हल: दिया है:
सिग्नल की चाल = प्रकाश की चाल = 3 x10⁸ m s^-1
सिग्नल पहुँचने में लगा समय = 5 मिनट = 5 x 60 = 300 सेकण्ड
अन्तरिक्ष यान की दूरी = सिग्नल की चाल x समय
= 3 x 10⁸ x 300 = 9 x 10¹⁰ m = 9 x 10⁷ km
अतः अन्तरिक्ष यान की अभीष्ट दूरी = 9 x 10¹⁰ m अर्थात् 9 x 10⁷ km.
प्रश्न शृंखला-3 # पृष्ठ संख्या 114
प्रश्न 1. आप किसी वस्तु के बारे में कब कहेंगे कि –

1. वह एकसमान त्वरण से गति में है।
2.  वह असमान त्वरण से गति में है।

उत्तर:
1.    जब वस्तु के वेग में परिवर्तन की दर समान हो।
2.    जब वस्तु के वेग में परिवर्तन मीटर असमान हो।
प्रश्न 2. एक बस की गति 5 s में 80 km h^-1 से घटकर 60 km h^-1 हो जाती है। बस का त्वरण ज्ञात कीजिए।
हल : ज्ञात है:

समय t = 5 s.
चूँकि हम जानते हैं कि v = u + at

अत: अभीष्ट त्वरण  = −109ms^-2. (मंदन)

प्रश्न 3. एक रेलगाड़ी स्टेशन से चलना प्रारम्भ करती है और एक समान त्वरण के साथ चलते हुए 10 मिनट में 40 km h^-1 की चाल प्राप्त करती है। इसका त्वरण ज्ञात कीजिए।

हल: ज्ञात है:
रेलगाड़ी का प्रारम्भिक वेग u = 0 m s^-1
रेलगाड़ी का अन्तिम वेग y= 40 km/h
=40×518=1009ms^-1
समय t = 10 मिनट = 10 x 6 = 600 s
चूँकि हम जानते हैं कि:
v = u + at

अतः अभीष्ट त्वरण =154ms^-1.

प्रश्न शृंखला 4 # पृष्ठ संख्या 118

प्रश्न 1. किसी वस्तु के एकसमान व असमान गति के लिए समय-दूरी ग्राफ की प्रकृति क्या होती है?

उत्तर: किसी वस्तु के एकसमान गति के लिए समय-दूरी ग्राफ एक सरल रेखा होगी, जबकि असमान गति के लिए समय-दूरी ग्राफ एक वक्र होगा।

प्रश्न 2. किसी वस्तु की गति के विषय में आप क्या कह सकते हैं जिसका दूरी-समय ग्राफ समय अक्ष के समानान्तर एक सरल रेखा है?
उत्तर: वस्तु स्थिर है।
प्रश्न 3. किसी वस्तु की गति के विषय में आप क्या कह सकते हैं जिसका चाल-समय ग्राफ समय अक्ष के समानान्तर एक सरल रेखा है?
उत्तर: वस्तु समान वेग से गति कर रही है।
प्रश्न 4. वेग-समय ग्राफ के नीचे के क्षेत्र से मापी गई राशि क्या होती है?
उत्तर: चली गई दूरी।
प्रश्न शृंखला 5 # पृष्ठ संख्या 121
प्रश्न 1. कोई बस विरामावस्था से चलना प्रारम्भ करती है तथा 2 मिनट तक 0.1 ms-2 के एकसमान त्वरण से चलती है। परिकलन कीजिए –
(a) प्राप्त की गई चाल
(b) तय की गई दूरी।
हल: ज्ञात है :
बस की प्रारम्भिक चाल u = 0 m s^-1 = 12 m s^-1 .
बस का त्वरण a = 0.1 m s^-2
यात्रा का समय = 2 मिनट = 120 s
ज्ञात करना है:
(a) प्राप्त की गई चाल v = ?
(b) तय की गई दूरी s = ?
(a)
∵ v = u + at
v = 0 + 0.1 x 120
v = 12 m s-1
अतः अभीष्ट चाल = 12 ms^-1 

= 720 m
अत: अभीष्ट दूरी = 720 m.

प्रश्न 2. कोई रेलगाड़ी 90 km h^-1 की चाल में चल रही है। ब्रेक लगाए जाने पर वह -0.5 m s^-2 का एकसमान त्वरण उत्पन्न करती है। रेलगाड़ी विरामावस्था में आने के पहले कितनी दूरी तय करेगी?

हल: ज्ञात है:
रेलगाड़ी की प्रारभिक चाल u = 90 km h^-1

u = 90 x 518 = 25 m s^-1

रेलगाड़ी की अन्तिम चाल v = 0 ms^-1

त्वरण a = -0.5 m s^-2

ज्ञात करना है:
तय की गयी दूरी s = ?

∵ 2as = v² – u²

⇒ 2 (-0.5) s = (0)² – (25)²

⇒ – s = 0 – 625

⇒ s = 625 m

अतः तय की गई अभीष्ट दूरी = 625 m.

प्रश्न 3. एक ट्रॉली एक आनत तल पर 2 m s^-2 के त्वरण से नीचे जा रही है। गति प्रारम्भ करने के 3 s के पश्चात् उसका वेग क्या होगा?

हल: ज्ञात है:
त्वरण a = 2 m s^-2

प्रारम्भिक वेग u = 0 m s^-1

समय अन्तराल t = 3 s

ज्ञात करना है:
अन्तिम वेग v = ?

∵ v = u + at

⇒ v = 0 + 2 x 3

⇒ v = 0 + 6 = 6 m s^-1

अतः अभीष्ट अन्तिम वेग = 6 ms^-1.

प्रश्न 4. एक रेसिंग कार का एकसमान त्वरण 4 ms-2 है। गति आरम्भ करने के 10 s पश्चात् उसका वेगक्या होगा?

हल: ज्ञात है:
त्वरण a = 4 m s^-2

प्रारम्भिक वेग u = 0 m s^-1

समयान्तराल t = 10 s

ज्ञात करना है:
अन्तिम वेग v = ?
⇒ v = u + at
⇒ v = 0 + 4 x 10
⇒ v = 0 + 40 = 40 m s^-1

अतः अभीष्ट अन्तिम वेग = 40 ms^-1.

प्रश्न 5. किसी पत्थर को ऊर्ध्वाधर ऊपर की ओर 5 ms^-1 के वेग से फेंका जाता है। यदि गति के दौरान पत्थर का नीचे की ओर दिष्ट त्वरण 10 ms^-2 

है, तो पत्थर के द्वारा कितनी ऊँचाई प्राप्त की गयी तथा उसे वहाँ पहुँचने में कितना समय लगा?

हल: ज्ञात है:
पत्थर का प्रारम्भिक वेग = 5 m s^-1

नीचे की ओर दिष्ट त्वरण = -a = 10 ms^-2

⇒ a = – 10 m s^-2

पत्थर का अन्तिम वेग v = 0 m s^-1

ज्ञात करना है:
प्राप्त ऊँचाई s = ?
लगा समय t = ?
अतः प्राप्त अभीष्ट ऊँचाई = 1.25 m एवं पहुँचने में लगा समय = 0.5 s.

∵ 2as = v² – u²

⇒ 2 (-10) s = (0)² – (5)²

⇒ – 20 s = – 25

⇒ s = 2520 = 1.25 m

एवं v = u + at
⇒ 0 = 5 + (- 10) t
⇒ 10 t = 5 ⇒ t = 510 = 0.55

पाठान्त अभ्यास के प्रश्नोत्तर

प्रश्न 1. एक एथलीट वृत्तीय पथ, जिसका व्यास 200 m है, का एक चक्कर 40 s में लगाता है। 2 मिनट 20 सेकण्ड के बाद वह कितनी दूरी तय करेगा? और उसका विस्थापन क्या होगा?
हल: ज्ञात है:
वृत्ताकार मार्ग का व्यास d = 200 m
एक चक्कर में लगा समय t₁ = 40 s
कुल समय = 2 min 20 s = 140 s
ज्ञात करना है:
दूरी = ?
विस्थापन = ?
एक चक्कर में चली दूरी = πd

चूँकि एथलीट 312 चक्कर लगाता है अतः उसकी अन्तिम स्थिति उसकी प्रारम्भिक स्थिति से वृत्ताकार मार्ग के व्यास के बराबर होगी। इसलिए विस्थापन = व्यास की लम्बाई = 200 m अतः अभीष्ट दूरी = 2200 m एवं अभीष्ट बिस्थापन = 200 m
प्रश्न 2. 300 m सीधे रास्ते पर जोसेफ जागिंग करता हुआ 2 min 30 s में एक सिरे A से B पर पहुँचता है और घूमकर 1 min में 100 m पीछे बिन्दु C पर पहुँचता है। जोसेफ की औसत चाल और औसत वेग क्या होंगे?
(a) सिरे A से सिरे B तक, तथा
(b) सिरे A से सिरे C तक।
हुल:

(a)

सिरे A से सिरे B तक कुल चली गई दूरी s1 = 300 m

A से B तक लगा कुल समय = 2 min 30 s = 120 + 30 = 150 s

सिरे A और B के बीच विस्थापन s = s₁ = 300 m

 अत: अभीष्ट औसत चाल = 2 ms^-1 एवं अभीष्ट औसत वेग = 2 ms^-1.

(b)
सिरे A से C तक चली कुल दूरी = s₁ + S₂ = 300 + 100 = 400 m

A से C तक विस्थापन = s₁ – S₂ = 300 – 100 = 200 m

A से C तक यात्रा में लगा कुल समय = t₁ + t₂ = 2 min 30 s + 1 min

= 3 min 30 s = 180 + 30 = 210 s

अतः अभीष्ट औसत चाल = 1.9 m s^-1 एवं अभीष्ट औसत वेग = 0.952 m s^-1. 

 प्रश्न 3. अब्दुल गाड़ी से स्कूल जाने के क्रम में औसत चाल को 20 km h^-1  पाता है। उसी रास्ते से लौटने के समय वहाँ भीड़ कम है और औसत चाल 30 km h^-1 है। अब्दुल की इस पूरी यात्रा में उसकी औसत चाल क्या है?

हल: मान लीजिए कि स्कूल की दूरी = x km

 अत: अभीष्ट औसत चाल = 24 km h^-1

प्रश्न 4. कोई मोटर बोट झील में विरामावस्था से सरल रेखीय पथ पर 3.0 m s^-2 के नियत त्वरण से 8.0 s तक चलती है। इस समय अन्तराल में मोटर बोट कितनी दूरी चलेगी?

हल: ज्ञात है:
मोटर बोट की प्रारम्भिक चाल u = 0 ms^-1

त्वरण a = 3.0 m s^-2

समय अन्तराल t = 8.0 s

ज्ञात करना है:
चली गई दूरी s = ?
हम जानते हैं कि:
s = ut + 12 at

⇒ s = o x 8 + 12 (3.0) x (8.0)²

⇒ s = 0 + 12 x 3 x 64
⇒ s = 3 x 32 = 96 m
अतः चली गयी अभीष्ट दूरी = 96 m. 

प्रश्न 5. किसी गाड़ी का चालक 52 km h^-1 की गति से चल रही कार में ब्रेक लगाता है तथा कार विपरीत दिशा में एकसमान दर से त्वरित होती है। कार 5 5 में रुक जाती है। दूसरा चालक 30 km h^-1 की गति से चलती हुई दूसरी कार पर धीमे-धीमे ब्रेक लगाता है तथा 10 s में कार रुक जाती है। एक ही ग्राफ पेपर पर दोनों कारों के लिए चाल-समय ग्राफ आलेखित करें। ब्रेक लगाने के पश्चात् दोनों में से कौन-सी कार अधिक दूरी तक जायेगी?

हल: दोनों कारों का अभीष्ट चाल-समय ग्राफ –

 

कार ‘A’ द्वारा चली गयी दूरी S_A = पहले त्रिभुज AOB का क्षेत्रफल

एवं कार ‘B’ द्वारा चली गयी दूरी S_B = दूसरे त्रिभुज COD का क्षेत्रफल
=12×30×518×10=3759m

अतः दूसरी कार अधिक दूरी तक जाएगी।

प्रश्न 6. संलग्न चित्र में तीन वस्तुओं A, B और C का दूरी-समय ग्राफ प्रदर्शित है। ग्राफ का अध्ययन करके निम्न प्रश्नों के उत्तर दीजिए –

1. तीनों में से कौन सबसे तीव्र गति से गतिमान है?
2. क्या ये तीनों किसी भी समय सड़क के एक ही बिन्दु पर होंगे? 
3. जिस समय B,A से गुजरती है उस समय तक C कितनी दूरी तय कर लेती है? 
4. जिस समय B, C से गुजरती है उस समय तक यह कितनी दूरी तय कर लेती है?

 उत्तर:

1. तीनों में से सबसे तीव्र गति से B गतिमान है क्योंकि B के ग्राफ का ढाल (प्रवणता) अधिकतम है, अतः उसकी चाल अधिकतम है।
2. ये तीनों कभी भी एक समय पर सड़क के एक ही बिन्दु पर नहीं होंगे।
3. C द्वारा तय की गई दूरी = 8 – 2 = 6 km
4. B द्वारा तय की गई दूरी = 6 – 0 = 6 km.

प्रश्न 7. 20 m की ऊँचाई से एक गेंद को गिराया जाता है। यदि उसका वेग 10 ms^-2 के एकसमान त्वरण की दर से बढ़ता है, तो यह किस वेग से धरातल से टकराएगी तथा कितने समय पश्चात् वह धरातल से टकराएगी?

हल: ज्ञात है:
गेंद का प्रारम्भिक वेग u = 0 m s^-1
ऊँचाई h = 20 m
त्वरण a = 10 ms^-2
ज्ञात करना है:
अन्तिम वेग v = ?
समयान्तराल t = ?

∵ v² = u² + 2as

⇒ v² = (0)² + 2 x 10 x 20

⇒ v² = 400 ⇒ v = √400 = 20 m s^-1

अब ∵ v = u + at
⇒ 20 = 0 + 10 x t
⇒ 10 t = 20 ⇒ t = 2010 = 2 s
अत: गेंद धरातल से 20 ms^-1 के वेग से 2 s पश्चात् टकराएगी।

प्रश्न 8. किसी कार का चाल-समय ग्राफ निम्न चित्र में दर्शाया गया है।
(a) पहले 4 s में कार कितनी दूरी तय करती है? इस अवधि में कार द्वारा तय की गई दूरी को ग्राफ में छायांकित क्षेत्र द्वारा दर्शाइए।  

(b) ग्राफ का कौन-सा भाग कार की एकसमान गति को दर्शाता है?
उत्तर:
(a) प्रथम 4 s में तय की गई दूरी को छायांकित क्षेत्र द्वारा प्रदर्शन।

 (b) ग्राफ का 6 5 से 10 s के बीच का भाग कार की एकसमान गति को दर्शाता है।
प्रश्न 9. निम्नलिखित में से कौन-सी अवस्थाएँ सम्भव हैं तथा प्रत्येक के लिए एक उदाहरण दें –
(a) कोई वस्तु जिसका त्वरण नियत हो परन्तु वेग शून्य हो।
(b) कोई वस्तु किसी त्वरण से गति कर रही है लेकिन समान चाल से।
(c) कोई वस्तु किसी निश्चित दिशा में गति कर रही हो तथा त्वरण उसके लम्बवत् हो?
उत्तर:
(a) यह अवस्था सम्भव है केवल स्वतन्त्रतापूर्वक गिरती वस्तु के प्रारम्भिक बिन्दु पर अथवा ऊर्ध्वाधर ऊपर की ओर फेंकी गयी वस्तु के अन्तिम बिन्दु पर जहाँ वस्तु का वेग शून्य तथा त्वरण गुरुत्वीय है।
(b) यह अवस्था सम्भव है जब कोई वस्तु वृत्ताकार मार्ग पर समान चाल से चल रही है जहाँ किसी भी बिन्दु पर त्वरण मार्ग के केन्द्र की ओर होगा।
(c) यह अवस्था केवल उस स्थिति में सम्भव है जब कोई वस्तु किसी दिशा में गति करना प्रारम्भ करती है तथा वृत्ताकार मार्ग पर चलती है उस समय उसका त्वरण उसकी गति की दिशा के लम्बवत् मार्ग के केन्द्र की ओर होगा।
प्रश्न 10. एक कृत्रिम उपग्रह 42250 km त्रिज्या की वृत्ताकार कक्षा में घूम रहा है। यदि वह 24 घण्टे में पृथ्वी की परिक्रमा करता है तो उसकी चाल का परिकलन कीजिए।
हल: ज्ञात है:
उपग्रह की कक्षा की त्रिज्या r = 42250 km
एक चक्कर में लगा समय t = 24 घण्टे
ज्ञात करना है:
चाल v = ?

 

 

 

 

 

 

 

 

अत: उपग्रह की अभीष्ट चाल = 11065.975 km h^-1

अर्थात् 3.074 km s^-1.

बहु-विकल्पीय प्रश्न

प्रश्न 1. कोई कण त्रिज्या (r) के वृत्ताकार पथ में गमन कर रहा है। अर्धवृत्त पूरा करने के पश्चात् उसका विस्थापन होगा –
(a) शून्य
(b) πr
(c) 2r
(d) 2πr
                                        उत्तर: (c) 2r
प्रश्न 2. एक पिण्ड वेग ‘u’ से ऊर्ध्वाधर ऊपर की ओर फेंका जाता है। इसके ऊपर उठने की अधिकतम ऊँचाई h होगी
 

 

 

 

 

 

उत्तर: (b) u22g
प्रश्न 3. किसी गतिमान पिण्ड के लिए विस्थापन तथा दूरी का आंकिक अनुपात क्या होता है?
(a) सदैव 1 से कम
(b) सदैव 1 के बराबर
(c) सदैव 1 से अधिक
(d) 1 के बराबर अथवा कम
                                        उत्तर: (d) 1 के बराबर अथवा कम
प्रश्न 4. यदि किसी पिण्ड का विस्थापन, समय के वर्ग के अनुक्रमानुपाती है तो वह वस्तु गमन करती हैं –
(a) एकसमान वेग से
(b) एकसमान त्वरण से
(c) बढ़ते त्वरण से
(d) घटते त्वरण से
                                        उत्तर: (b) एकसमान त्वरण से
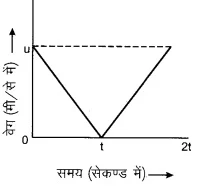
प्रश्न 5. दिए गए v – t ग्राफ (संलग्न चित्र 8.7) से यह निष्कर्ष निकाल सकते हैं कि पिण्ड –

(a) एकसमान गति कर रहा है
(b) विराम अवस्था में है
(c) असमान गति कर रहा है
(d) एकसमान त्वरण से गति कर रहा है
                                        उत्तर: (a) एकसमान गति कर रहा है

प्रश्न 6. मान लीजिए कोई लड़का 10 m s^-1 की नियत चाल से चल रहे ‘मेरीगोराडण्ड’ झूले पर सवारी करने का आनन्द ले रहा है। इससे ज्ञात होता है कि वह लड़का –

(a) विराम में है

(b) बिना त्वरण के गति कर रहा है

(c) त्वरित गति में है

(d) एकसमान वेग से गमन कर रहा है

                                        उत्तर: (c) त्वरित गति में है

प्रश्न 7. v – t ग्राफ द्वारा घेरा गया क्षेत्रफल किसी भौतिक राशि को निरूपित करता है, जिसका मात्रक है –

(a) m²

(b) m

(c) m³

(d) m s^-1

                                        उत्तर: (c) m³

प्रश्न 8. चार कार A, B, C तथा D किसी समतल सड़क पर गति कर रही हैं। इनके दूरी-समय ग्राफ संलग्न चित्र 8.8 में दर्शाये गए हैं। सही कथन चुनिए।

(a) कार A की चाल कार D से अधिक है
(b) कार B सबसे धीमी है
(c) कार D की चाल कार C से अधिक है
(d) कार C सबसे धीमी है।
                                        उत्तर: (b) कार B सबसे धीमी है
प्रश्न 9. संलग्न चित्र का कौन-सा ग्राफ एकसमान गति का सही निरूपण करता है?

                                        उत्तर: (a)
प्रश्न 10. वेग-समय ग्राफ की प्रवणता से प्राप्त होता है –
(a) दूरी
(b) विस्थापन
(c) त्वरण
(d) चाल
                                        उत्तर: (c) त्वरण
प्रश्न 11. नीचे दिए गए प्रकरणों में से किसमें चली गई दूरी तथा विस्थापन के परिमाण समान होते हैं –
(a) यदि कार सीधी सड़क पर गमन कर रही है
(b) यदि कार वृत्ताकार पथ पर गमन कर रही है
(c) लोलक इधर-उधर गति कर रहा है
(d) पृथ्वी सूर्य की परिक्रमा कर रही है
                                        उत्तर: (a) यदि कार सीधी सड़क पर गमन कर रही है
प्रश्न 12. वेग परिवर्तन की दर है –
(a) चाल
(b) त्वरण
(c) दाब
(d) बल
                                        उत्तर: (b) त्वरण

रिक्त स्थानों की पूर्ति

1. वेग परिवर्तन की दर …………….. कहलाती है।
2. विस्थापन की दर …………… कहलाती है।
3. वेग एक …………… राशि है।
4. विस्थापन एक …………… राशि है।
5. चाल एक ………….. राशि है।
6. दूरी एक …………….. राशि है।
7. यदि वस्तु की गति का पथ सरल रेखीय हो, तो ऐसी गति …………… कहलाती है।
8. त्वरण एक …………….. राशि है।
9. ऋणात्मक त्वरण …………….. कहलाता है।
10. वे भौतिक राशियाँ जिन्हें व्यक्त करने के लिए परिमाण एवं दिशा दोनों की आवश्यकता होती है, ……. कहलाती है।
11. वे भौतिक राशियाँ जिन्हें व्यक्त करने के लिए केवल परिमाण की आवश्यकता होती है, …………. कहलाती हैं।

उत्तर:

1. त्वरण
2. वेग
3. सदिश
4. सदिश
5. अदिश
6. अदिश
7. सरल रेखीय गति
8. सदिश
9. मंदन
10. सदिश
11. अदिश

सही जोड़ी बनाना :-

उत्तर:

1. → (iii)
2. → (iv)
3. → (v)
4. → (vi)
5. → (i)
6. → (ii)

सत्य / असत्य कथन

1. प्रति सेकण्ड विस्थापन को चाल कहते हैं।
2. वेग परिवर्तन की दर त्वरण कहलाती है।
3. विस्थापन सदैव दूरी से अधिक होता है।
4. ऋणात्मक त्वरण को मंदन कहते हैं।
5. गतिमान वस्तु का वेग कभी भी शून्य नहीं हो सकता।

उत्तर:

1. असत्य
2. सत्य
3. असत्य
4. सत्य
5. असत्य।

एक शब्द / वाक्य में उत्तर

प्रश्न 1. सरल आवर्त गति का उदाहरण दीजिए।
उत्तर: लोलक की गति।
प्रश्न 2. कोई पिण्ड एक वृत्ताकार मार्ग पर गति करता हुआ एक पूरा चक्कर लगाता है। उसका विस्थापन क्या होगा?
उत्तर: शून्य।
प्रश्न 3. विस्थापन/समय अन्तराल व्यंजक किस भौतिक राशि को व्यक्त करते हैं?
उत्तर: वेग।
प्रश्न 4. वेग परिवर्तन की दर क्या कहलाती है?
उत्तर: त्वरण।
प्रश्न 5. प्रति सेकण्ड वेग में होने वाली कमी को क्या कहते हैं?
उत्तर: मंदन।

अति लघु उत्तरीय प्रश्न

प्रश्न 1. एकसमान गति से क्या समझते हो ? उदाहरण दीजिए।
उत्तर: एकसमान गति:- “जब कोई वस्तु समान अन्तराल में समान दूरी तय करती है, तो उस वस्तु की गति को एकसमान गति कहते हैं।”
उदाहरण: पृथ्वी के चारों ओर चन्द्रमा की गति।
प्रश्न 2. असमान गति से क्या तात्पर्य है? उदाहरण दीजिए।
उत्तर: असमान गति:- “जब कोई वस्तु समान समयान्तराल में असमान दूरी तय करती है तो उस वस्तु की गति को असमान गति कहते हैं।”
उदाहरण: सड़क पर चलती कार की गति।
प्रश्न 3. सरल रेखीय गति की परिभाषा दीजिए।
उत्तर: सरल रेखीय गति:- “यदि किसी पिण्ड की गति का पथ एक सरल रेखा हो, तो उस पिण्ड की गति को सरल रेखीय गति कहते हैं।”
प्रश्न 4. अदिश राशियों को परिभाषित कीजिए। उदाहरण भी दीजिए।
उत्तर: अदिश राशियाँ:- “वे भौतिक राशियाँ जिनका व्यक्त करने के लिए केवल परिमाण की आवश्यकता होती है, दिशा की नहीं। अदिश राशियाँ कहलाती हैं।”
उदाहरण: दूरी, चाल, घनत्व आदि।
प्रश्न 5. सदिश राशियों को परिभाषित कीजिए। उदाहरण भी दीजिए।
उत्तर: सदिश राशियाँ:- “वे भौतिक राशियाँ जिन्हें व्यक्त करने के लिए परिमाण के साथ-साथ दिशा की भी आवश्यकता होती है, सदिश राशियाँ कहलाती हैं।”
उदाहरण: विस्थापन, वेग, त्वरण आदि।
प्रश्न 6. चाल किसे कहते हैं? इसका मात्रक लिखिए।
उत्तर: चाल:- “किसी वस्तु द्वारा इकाई समय अन्तराल में चली गई दूरी उस वस्तु की चाल कहलाती है।”

मात्रक: - मीटर प्रति सेकण्ड (m s^-1)

प्रश्न 7. औसत चाल से क्या समझते हो?
उत्तर: औसत चाल:- किसी समय अन्तराल में तय की गयी कुल दूरी और समय अन्तराल के अनुपात को औसत चाल कहते हैं।”

प्रश्न 8. वेग की परिभाषा दीजिए तथा इसका मात्रक भी लिखिए।
उत्तर: वेग-“समय के साथ विस्थापन की दर को वेग कहते हैं।”

मात्रक:- मीटर प्रति सेकण्ड (ms-1)
प्रश्न 9. असमान (परिवर्ती) वेग किसे कहते हैं?
उत्तर: असमान (परिवर्ती) वेग:- “जब कोई गतिशील वस्तु बराबर समय-अन्तराल में बराबर दूरी तय करे लेकिन उसकी गति की दिशा बदल जाये अथवा बराबर समय अन्तराल में बराबर दूरी तय नहीं करे तो उस वस्तु का वेग असमान (परिवर्ती) वेग कहलाता है।”
प्रश्न 10. औसत वेग किसे कहते हैं?
उत्तर: औसत वेग:- “किसी भी गतिशील वस्तु के कुल विस्थापन एवं समय-अन्तराल के अनुपात को औसत वेग कहते हैं।”

प्रश्न 11. त्वरण किसे कहते हैं? इसका मात्रक लिखिए।
उत्तर: त्वरण:- “वेग वृद्धि की समय के साथ दर को त्वरण कहते हैं।”

मात्रक:- मीटर प्रति सेकण्ड² (m s^-2)

प्रश्न 12. मंदन किसे कहते हैं? मंदन एवं त्वरण में क्या सम्बन्ध है?

उत्तर: मंदन: -“किसी वस्तु के वेग में कमी एवं समय अन्तराल के अनुपात को मंदन कहते हैं।” मंदन एवं त्वरण में सम्बन्ध:- ऋणात्मक त्वरण ही मंदन होता है।

प्रश्न 13. वत्तीय गति किसे कहते हैं ? उदाहरण दीजिए।

उत्तर: वृत्तीय गति:- “जब कोई गतिशील वस्तु किसी वृत्ताकार मार्ग पर गति करती है तो उस वस्तु की गति वृत्तीय गति कहलाती है।

उदाहरण:- वृत्ताकार मार्ग पर साइकिल चलाते सवार की गति।

प्रश्न 14. एकसमान वृत्तीय गति किसे कहते हैं?

उत्तर: एकसमान वृत्तीय गति:- “जब कोई वस्तु समान चाल से किसी वृत्ताकार मार्ग पर गति करती है तो उसकी गति को एकसमान वृत्ताकार गति कहते हैं।”

प्रश्न 15. किसी गतिशील पिण्ड का दिए गए समय-अन्तराल में विस्थापन शून्य है। क्या इसके द्वारा चली गयी दूरी भी शून्य होगी? अपने उत्तर की पुष्टि कीजिए।

उत्तर:- नहीं। वृत्ताकार मार्ग पर गतिमान कोई पिण्ड अपनी प्रारम्भिक स्थिति में लौट आता है तो उसका विस्थापन तो शून्य होता है लेकिन चली गयी दूरी शून्य नहीं है।

लघु उत्तरीय प्रश्न

प्रश्न 1. गति के समीकरण किसी एकसमान वेग से गमन करते पिण्ड के लिए किस प्रकार परिवर्तित होते हैं?
हल:
∵ एकसमान वेग की स्थिति में त्वरण a = 0 m s^-2

∴ गति के समीकरण –

(1) v = u + at = u + 0 x t = v = u.

(2) s = ut + 12at² = ut + 12 x 0 x t² = s = ut.

(3) v² = u² + 2as = u² + 2 x 0 x s = v = u.

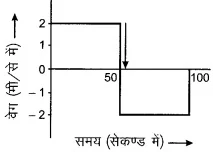
प्रश्न 2. कोई बालिका किसी सरल रेखीय पथ के अनुदिश चलकर पत्रपेटी में पत्र डालती है और वापस अपनी प्रारम्भिक स्थिति में लौट आती है। उसकी गति का दूरी-समय ग्राफ संलग्न चित्र में दर्शाया गया है। उसकी गति के लिए वर्ग-समय ग्राफ खींचिए। 

हल:

 

अतः अभीष्ट वेग-समय ग्राफ

प्रश्न 3. कोई कार विराम अवस्था से गति प्रारम्भ करके x – अक्ष के अनुदिश नियत त्वरण a’ = 5. m s^-2 से 85 तक गमन करती हैं। इसके पश्चात् यदि कार नियत वेग से गति करती रहती है, तो विराम से गति प्रारम्भ करने की पश्चात् 12 सेकण्ड में यह कितनी दूरी तय करेगी?हल: ज्ञात है:
प्रारम्भिक वेग u = 0 m s^-1

त्वरण a = 5 m s^-2

समय (त्वरित गति) t₁ = 8 s

अन्तिम समय t₂ = 12 s

प्रथम 8 सेकण्ड में चली दूरी

x₁ = ut₁ + 12at₁²

= 0 x 8 + 12 x 5 x (8)²

= 160m

v₁ = u + at

= 0 + 5 x 8 = 40 m s^-1

8 s बाद कार एकसमान गति u = v1 = 40 m s^-1 से गति करेगी। अब अन्तिम 4 s (8वें सेकण्ड से 12वें सेकण्ड तक) में चली दूरी

x₂ = वेग x समय = 40 x (12 – 8)= 40 x 4= 160 m

कुल दूरी x = x₁ + x₂ = 160 m + 160 m = 320 m

अत: अभीष्ट दूरी = 320 m.

प्रश्न 4. कोई मोटरसाइकिल सवार A से B तक 30 km h^-1 की एकसमान चाल से जाता है और 20 km h^-1 की चाल से वापस लौटता है। औसत चाल ज्ञात कीजिए।
हल: ज्ञात है:
मोटरसाइकिल की जाते समय चाल = 30 km h^-1

एवं उसकी आते समय चाल = 20 km h^-1

माना A से B के बीच की दूरी x km है तो  

अतः अभीष्ट औसत चाल = 24 km h^-1.

प्रश्न 5. किसी साइकिल सवार की गति को वेग-समय ग्राफ (संलग्न चित्र) में दर्शाया गया है। इस गति का त्वरण, वेग तथा 15 5 में साइकिल सवार द्वारा तय की गई दूरी ज्ञात कीजिए।

हल: त्वरण: चूँकि साइकिल 20 m s^-1 के एकसमान वेग से गतिमान है अर्थात् वेग में परिवर्तन नहीं है।

अतः त्वरण = 0 m s^-2

वेग: ग्राफ के पाठांक के अनुसार वेग = 20 ms^-1 है अतः साइकिल का वेग = 20 m s^-1 प्रथम 15 s में साइकिल द्वारा तय की गयी दूरी संलग्न ग्राफ में छायांकित क्षेत्र से दिखाई गई है जिसका क्षेत्रफल = 20 x 15 = 300m । 

इसलिए साइकिल द्वारा तय की गई दूरी = 300 m.

अतः अभीष्ट त्वरण = 0 m s^-2, वेग = 20 ms^-1 एवं तय की गई दूरी = 300 m.

प्रश्न 6. उस पत्थर का वेग-समय ग्राफ खींचिए जो ऊर्ध्वाधर ऊपर फेंका जाता है और अधिकतम ऊँचाई पर पहुँचने के पश्चात् अधोमुखी वापस आ रहा है।
हल: माना पत्थर प्रारम्भिक वेग से ऊपर की ओर ऊर्ध्वाधर फेंका जाता है जो गुरुत्वीय मंदन (ऋणात्मक गुरुत्वीय त्वरण) से गति करता है। अधिकतम ऊँचाई पर इसका वेग शून्य हो जाता है। पुनः यह गुरुत्वीय धनात्मक त्वरण से नीचे आता है। इसका समय-वेग अथवा वेग-समय ग्राफ संलग्न चित्र में दिखाया गया है।
अतः अभीष्ट वेग-समय ग्राफ का उपर्युक्त चित्र है।

प्रश्न 7. कोई पिण्ड 150 m की ऊँचाई से विश्राम से गिराया जाता है तथा उसी क्षण किसी अन्य पिण्ड को 100 m की ऊँचाई से विराम से गिराया जाता है। यदि दोनों प्रकरणों में त्वरण समान है तो 25 के पश्चात् इनकी ऊँचाई में क्या अन्तर है? समय में परिवर्तन के साथ इस ऊँचाई के अन्तर में क्या परिवर्तन होता है?
हल: दोनों पिण्डों की प्रारम्भिक ऊँचाई में अन्तर = (150 m – 100 m) = 50 m
प्रथम पिण्ड द्वारा 2 s में चली गई दूरी

s₁ = 0 x 2 + 12 x g (2)² = 2g m

इस पिण्ड की ऊँचाई h₁ = (150 – 2g) m

दूसरे पिण्ड द्वारा 2 s में चली गई दूरी

s₂ = 0 x 2 + 12g (2)₂ = 2gm [∴ u= 0 दिया है]

इस पिण्ड की ऊँचाई h₂ = (100 – 2g) m

इसलिए दोनों पिण्डों की ऊँचाइयों में अन्तर = (150 – 2g) – (100 – 2g) m

= 150 – 100 = 50 m = प्रारम्भिक ऊँचाई में अन्तर

अतः दोनों पिण्डों की (2s पश्चात्) ऊँचाइयों में अभीष्ट अन्तर = 50 m
समय परिवर्तन के साथ इस ऊँचाई के अन्तर में कोई परिवर्तन नहीं होगा।

प्रश्न 8. 5 x 10⁴ m s^-1 के वेग से गतिमान कोई इलेक्ट्रॉन एक समान विद्युत क्षेत्र में प्रवेश करके अपनी प्रारम्भिक गति की दिशा में 104 ms^-2 का एकसमान त्वरण अर्जित करता है।
(i) वह समय परिकलित कीजिए जिसमें यह इलेक्ट्रॉन अपने प्रारम्भिक वेग का दो गुना वेग अर्जित करेगा।
(ii) इस समय में इलेक्ट्रॉन कितनी दूरी तय करेगा?
हल: ज्ञात है:
इलेक्ट्रॉन का प्रारम्भिक वेग u =5 x 10⁴ m s^-1

इसका अन्तिम वेग v = 2u = 10 x 10⁴ m s^-1

त्वरण a= 1 x 10⁴ m s^-2

ज्ञात करना है:
समय t = ?
तय दूरी x = ?

(i)
∵ v = u + at

⇒ 10 x 10⁴ = 5 x 10⁴ + 1 x 10⁴ t

⇒ 10⁴ t = 10 x 10⁴ – 5 x 10⁴ = 5 x 10⁴

t = 5 s.

(ii)

∵ x = ut + 12at²

⇒ x = 5 x 10⁴ x 5 + 12 x 10⁴ x (5)²

= 25 x 10⁴ + 252 x 10⁴

= (25 + 12.5) x 10⁴ m

= 37.5 x 10⁴ m

अतः अभीष्ट समय = 5 s एवं अभीष्ट दूरी = 37.5 x 10⁴ m.

प्रश्न 9. एकसमान त्वरण से गतिमान किसी पिण्ड द्वारा चौथे तथा पाँचवें सेकण्ड के अन्तराल के बीच दूरी के लिए सम्बन्ध व्युत्पन्न कीजिए।
हल: मान लीजिए पिण्ड का प्रारम्भिक वेगu m s^-1 एवं एकसमान त्वरण a m s^-2 है तो

∵ s = ut + 12 at²

⇒ S₄ = u x 4+ 12a (4)² = 4u + 8a

⇒ 5_s = u + 5 + 12a (5)² = 5u + 12.5a

⇒ 5₅ – S₄ = u + 4.5 a = u + 92a

अत: चौथे एवं पाँचवें सेकण्ड के अन्तराल में चली गई अभीष्ट दूरी = (u+92a)m.

प्रश्न 10. दो गेंदें एक ही क्षण अपने-अपने क्रमशः प्रारम्भिक वेगों u₁ तथा u₂ से ऊपर की ओर ऊर्ध्वाधर दिशा में फेंकी जाती हैं। सिद्ध कीजिए कि इनके द्वारा तय की गई ऊँचाइयाँ u₁² : u₂² के अनुपात में होंगी। (यह मान लीजिए कि उपरिमुखी त्वरण – g तथा अधोमुखी त्वरण + g है।)

हल:हम जानते हैं कि उपरिमुखी गति के लिए v² = u² – 2gh

परन्तु उच्चतम बिन्दु पर v = 0

इसलिए 0 = u² – 2gh

 

इससे सिद्ध होता है कि अभीष्ट गेंदों द्वारा तय की गई ऊँचाइयाँ u₁² : u₂² के अनुपात में होगी।

प्रश्न 11. दूरी एवं विस्थापन में अन्तर लिखिए।

उत्तर: दूरी एवं विस्थापन में अन्तर:-

दूरी :-

1. तय किए गए मार्ग की कुल लम्बाई दूरी कहलाती है।
2. यह एक अदिश राशि है।
3. दूरी कभी ऋणात्मक एवं शून्य नहीं हो सकती।
4. दो और अधिक दूरियों का परिणमी सदैव धनात्मक होता है।
5. दूरी वस्तु द्वारा चले गये मार्ग पर निर्भर करती है।

विस्थापन :-

1. प्रारम्भिक एवं अन्तिम स्थिति के बीच की न्यूनतम दूरी निश्चिम दिशा में विस्थापन कहलाती है।
2. यह एक सदिश राशि है।
3. विस्थापन ऋणात्मक भी हो सकता है और शून्य भी।
4. दो या अधिक विस्थापनों का परिणामी ऋणात्मक, धनात्मक एवं शून्य भी हो सकता है।
5. विस्थापन चले गए मार्ग पर निर्भर नहीं करता है।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1. ग्राफीय विधि से निम्न गति के समीकरणों की स्थापना कीजिए –

(1) v = u + at

(2) s = ut + 12at²

(3) v² – u² = 2as.

हल: मान लीजिए कि एकसमान त्वरण a से गतिमान किसी वस्तु का प्रारम्भिक वेग u एवं t सेकण्ड के समय अन्तराल के बाद अन्तिम वेग v है तथा इस समय अन्तराल में वस्तु द्वारा तय की गई दूरी s है तथा उसका वेग-समय ग्राफ संलग्न चित्र में दिया है।
तो ग्राफ के अनुसार BC = v, OA = u तथा OC =t
तब BD = BC – DC = BC – OA = v – u
तथा AD = OC = t होगा।
चूँकि त्वरण = वेग-समय ग्राफ की प्रवणता = BDAD
⇒ a = v − ut
⇒ v – u = at
⇒ v = u + at …(1)
चूँकि वेग-समय ग्राफ में ग्राफ AB के नीचे घिरे क्षेत्र OABC द्वारा दूरी प्राप्त की जाती है।
इसलिए दूरी s = क्षेत्र. (OABC) = क्षेत्र. (आयत OADC) + क्षेत्र. (AABD)
= OC x OA+ 12AD x BD
= t x u + 12 x t x (v – u)
⇒ s = ut + 12(at) [∵ समीकरण (1) में v – u = at]

⇒ s = ut + 12at² ….(2)

दूरी s = क्षेत्र. (समलम्ब चतुर्भुज OABC)  

इस प्रकार गति के अभीष्ट समीकरणों –

1. V = u + at
2. s = ut + 12at², एवं
3. 2as = v – u का ग्राफीय विधि से सत्यापन हुआ।

प्रश्न 2. कोई पिण्ड विराम से गति प्रारम्भ करके पहले 2 5 में 20 m तथा अगले 45 में 160 m चलता है। प्रारम्भ से 7 s पश्चात् उसका वेग क्या होगा?
हल: ज्ञात है:
प्रारम्भिक वेग u = 0

प्रथम t₁ = 2 s में दूरी s₁ = 20 m

अगले t₂ = 4 s में दूरी s₂ = 160 m

प्रारम्भ से समय t = 7.

s = ut + 12at²

⇒ 20 = 0 x 2 + 12a (2)²

⇒ 20 = 2a

⇒ a = 202 = 10^-2

2 s पश्चात् वेग v₁ है तो

v₁ = u + at

= 0 + 10 x 2 = 20 m s^-1

यह अगले 4 s के लिए प्रारम्भिक वेग / होगा। अब अगले 4 s में चली दूरी

S₂ = u’ t₂ + 12a (t₂)

⇒ 160 = 20 x 4+ 12a'(4)²

⇒ 160 = 80 + 8a’ ⇒ 8a’ = 160 – 80 = 80

a’ = 808 = 10 m s^-2

इस तरह हम देखते हैं कि त्वरण एकसमान है।
अब मान लीजिए 7 s पश्चात् वेग v है, तो

v =u+ at

v = 0 + 10 x 7 = 70 m s^-1

अतः 75 के पश्चात् अभीष्ट वेग = 70 m s^-1.

_______________________

महत्वपूर्ण नोट (important note):- इस अध्याय की पीडीएफ फाईल डाउनलोड़ करने के लिये नीचे दीये बटन पर क्लिक करे।
To download the PDF file of this chapter, click on the button given below.

निर्देश (Instruction):-
बटन पर क्लिक करे।
Click on the button.
10 सेकेण्ड़ के बाद डाउनलोड बटन ओपन होगा।
After 10 seconds the download button will open.
डाउनलोड़ बटन पर क्लिक करे।
Click on the download button.
15 सेकण्ड के बाद पीडीएफ फाईन ओपन होगी।
After 15 seconds the PDF will open fine.

_______________________